R
E C - T E C
ACCIDENT .
. . . . RECONSTRUCTION
. . . . . .
SOFTWARE
"when performance counts"
George M. Bonnett, J.D.
REC-TEC LLC
The graphics and mathematical computations used throughout this article were generated using REC-TEC Professional - Version V accident reconstruction software from REC-TEC LLC.
The reader may find a working knowledge of both linear momentum and vector sum analysis to be beneficial in understanding the concepts presented in this manual. Impact Velocity from Conservation of Linear Momentum and Conservation of Linear Momentum Using Vector Sum Analysis, both by W. A. Kennedy, offer an excellent background for Vector Momentum Analysis. These manuals are available through I.P.T.M., University of North Florida, Jacksonville, Florida 32224-2645.
Copyright © 1993 by George M. Bonnett, J.D. All rights reserved. No part of this publication may be reproduced or transmitted in any form, or any means, electronic or mechanical, including photography, recording, or by any information storage and retrieval system, without prior permission in writing from the copyright holder.
Published and distributed by:
REC-TEC LLC
George M. Bonnett, J.D.
INTRODUCTION: Vector Momentum Analysis is an effective method of solving linear momentum problems for the post impact data resulting from known, or given, impact information. This is advantageous during any in depth analysis of vehicles in collision.
COORDINATE SYSTEMS: The most widely used systems for both Cartesian and polar coordinates are the RIGHT HAND COORDINATE SYSTEM (RHCS) and the LEFT HAND COORDINATE SYSTEM (LHCS).
The two (2) systems share several common attributes:
Differences between the systems are:
The LHCS will be used in all future discussions and diagrams. The same scale will be used on both axes. This is for convenience only. It is not required by the LHCS, but will allow placement of a protractor over the diagrams that may assist in comprehending some of the information being presented.
VECTORS: A clear understanding of the concept of vectors and their components is mandatory to an understanding of accident reconstruction in general, and linear momentum in particular. A vector is a graphical representation of a physical action that has both magnitude and direction. A scalar is an algebraic quantity having magnitude, but not direction. Speed without direction is a scalar. Scalars can have units, and perhaps an algebraic sign, but no direction. Speed with direction (often referred to as velocity) is a VECTOR. In addition to magnitude and direction, a vector requires a sense (+ or -) to the direction.
Scalars are added mathematically. It is simple addition. Vectors must be added using the parallelogram rule. They must be added geometrically and not mathematically. The vector addition law states that if the arrows representing a set of vectors are laid tail to head in any order, the vector sum (the resultant vector) is represented by the arrow that connects the tail of the first to the head of the last.
While adequately illustrating the concept, it is cumbersome to carry a ruler and protractor in order to add vectors, and often very inaccurate. The method of components is more convenient in that it reduces all vector additions to the addition of perpendicular vectors.
CONSTANTS: Everything will be discussed in reference to the origin (0,0), providing a constant frame of reference. None of the problems will contain labels for either weights or speeds (velocities). They have no bearing on the subject matter, serving only to confuse, and will therefore be eliminated from all future discussions.
While purists may raise eyebrows, the angles involved in the collision will be referred to as A1, A2, A3, A4, and not by their traditional Greek names. The new names are more easily identified with the associated vector by both the expert and the lay person (judge or jury).
In order to simplify understanding of the concepts involved, the following values will be held constant unless otherwise stated in the problem:
Vehicle #1
Vehicle #2
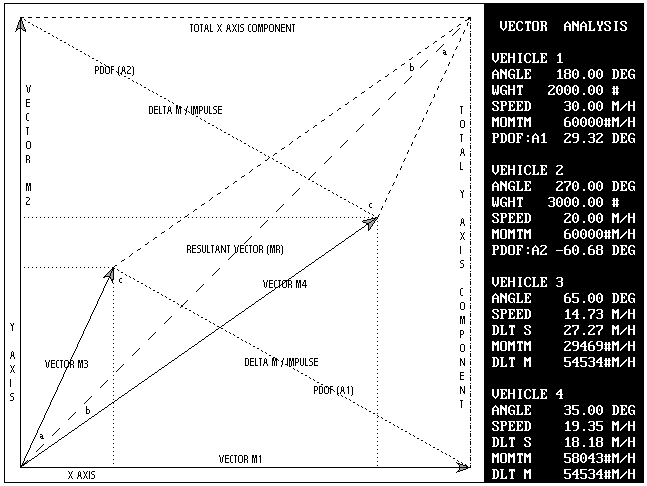
METHODOLOGY: Vector momentum analysis combines linear momentum, vector sum analysis, and trigonometry to solve the post impact data that results from given impact information. The impact data is used to compute a resultant vector (Mr) as well as the orientation angle (AO) of the resultant vector. The resultant vector (Mr) and the two (2) post impact momentum vectors (M3 and M4) form a triangle. The resultant vector is a (known) side of this triangle. Two (2) angles of the triangle (a and b) have a direct correlation to the relationship between the departure angles (A3 and A4) and the orientation angle (AO) of the resultant vector.
The Law of Sines and the Law of Cosines will permit the computation of the sides and the angles of a triangle if the following can be determined:
1. Two (2) angles and one (1) side;
2. Two (2) sides and one (1) angle;
3. Three (3) sides.
Once results are obtained using vector momentum analysis, the post impact data can then be used to generate impact velocities using linear momentum. The results obtained from linear momentum should be identical to the input data used for vector momentum analysis. Vector sum analysis may be used as a graphical check on the mathematical results obtained from both vector momentum analysis and linear momentum.

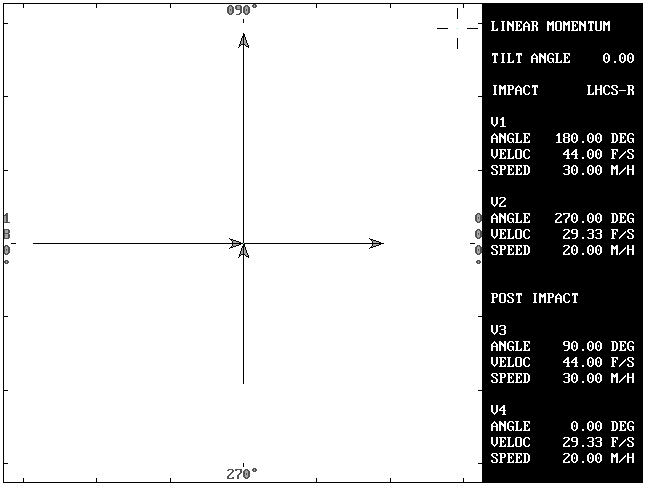
PROBLEMS: Three basic problems will be used in examining the concept of vector momentum analysis. The problems will consist of collisions with the approach angles between vehicle #1 and vehicle #2 of: (1) 90 degrees; (2) less than 90 degrees; and (3) greater than 90 degrees.
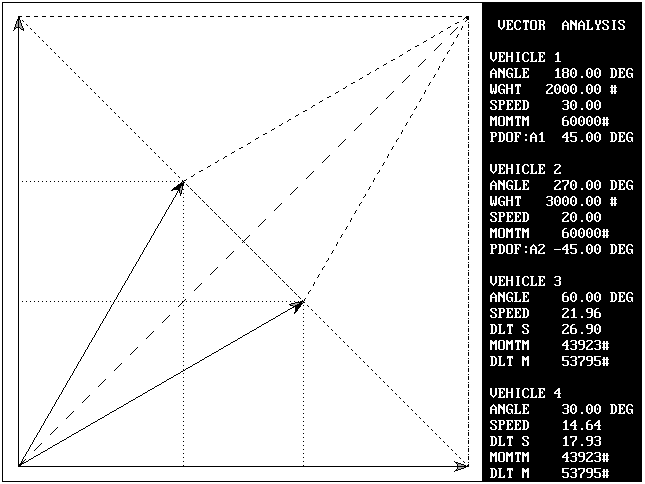
1. If vehicle #1 has a known departure angle of 60 degrees (A3), and vehicle #2 has a known departure angle of 30 degrees (A4) then vector M3 would have an angle of 60 degrees (A3) and vector M4 would have an angle of 30 degrees (A4). The vectors M3 and M4 can be added by joining the tail of M4 to the head of M3. M4 and M3 can be also be added by joining the tail of M4 to the head of M3, forming a parallelogram. (Review the rule for vector addition on page 2.) The resultant vector (Mr) divides the parallelogram into two similar triangles that share a common side. This may now be treated as a trigonometry problem. Since two (2) angles (A3 and A4) and a side (Mr) are known, The Law of Sines can be used to solve for sides (M3 and M4). This method will be used in solving Problem 1C.
2. If, instead of angles (A3 and A4), the departure velocities (V3 and V4) are known, the magnitude of the two (2) momentum vectors (M3 and M4) can be obtained by multiplying the velocities (V3 and V4) by their respective weights (W1 and W2). All three (3) sides of the triangle(s) are then known, and by using the Law of Cosines, the respective departure angles (A3 and A4) can be determined. This method will be used in solving Problem 2.
3. If only one (1) of the departure angles (A3 or A4) and one (1) of the departure velocities (V3 or V4) is known, the other two (2) unknowns can be solved by using the Law of Cosines. Some of the combinations may involve the use of a quadratic equation. This results in an ambiguous case that has two (2) possible solutions. There is only one (1) correct solution due to the nature of the triangle involved. This will be discussed further in Problem 3B. These methods (with and without the quadratic) will be used in solving Problems 3A and 3B.
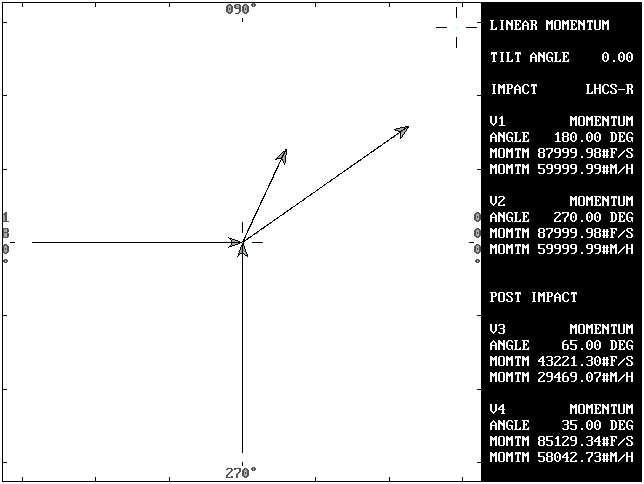
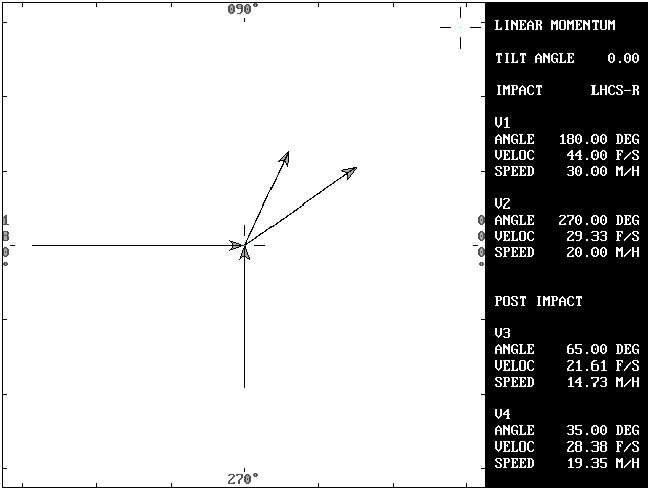
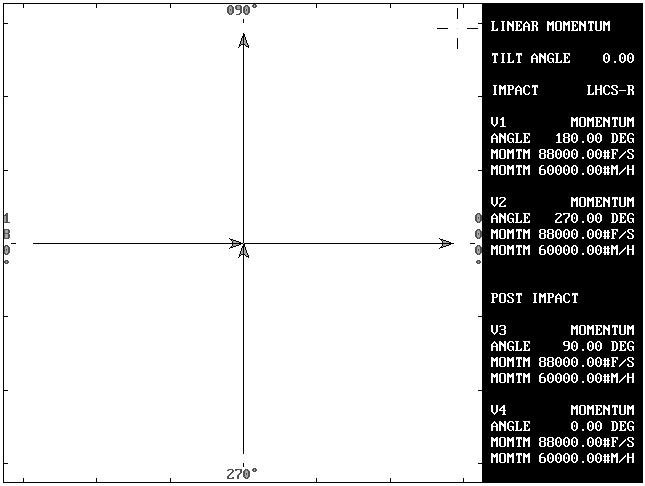
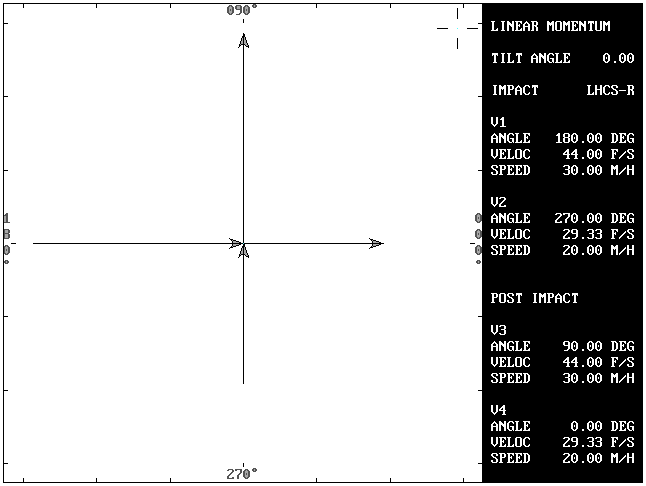
Problem 1A: In linear momentum, the post impact velocities of vehicle #1 (V3) and vehicle #2 (V4) are used to solve for the respective impact velocities (V1 and V2).
V1, and therefore M1,is always aligned with the X axis. It never has a vertical (Y axis) component of velocity. The sine of angle A1 (180 degrees) is always zero (0) and the cosine is always -1. Solving for V2 first eliminates a variable and makes the solution possible. This alignment makes it possible to solve a linear momentum problem that is not collinear (inline).
Conservation of Linear Momentum
M1*V3 + M2*V4 = M1*V1 + M2*V2
M = W/g ; substitute for M:
(W1*V1)/g + (W2*V2)/g = (W1*V3)/g + (W2*V4)/g
Multiply by g:
W1*V1 +W2*V2 = W1*V3 + W2*V4
Solving for V2:
W1*V1*sin(A1) + W2*V2*sin(A2) = W1*V3*sin(A3) + W2*V4*sin(A4)
V2 = (W1*V3*sin(A3) + W2*V4*sin(A4) - W1*V1*sin(A1)) / W1*sin(A2)
V2 = 2000*20*-1 + 3000*30*0 - 2000*V1*0 / 2000*-1
V2=(-40000 + 0 - 0) / -2000
V2 = 20
Solving for V1:
W1*V1*cos(A1) + W2*V2*cos(A2) = W1*V3*cos(A3) + W2*V4*cos(A4)
V1 = (W1*V3*cos(A3) + W2*V4*cos(A4) - W2*V2*cos(A2)) / W1*cos(A1)
V1 = 2000*20*0 + 3000*30*0 + 3000*20*-1 / 2000*-1
V1=(-60000 + 0 - 0) / -2000
V1 = 30
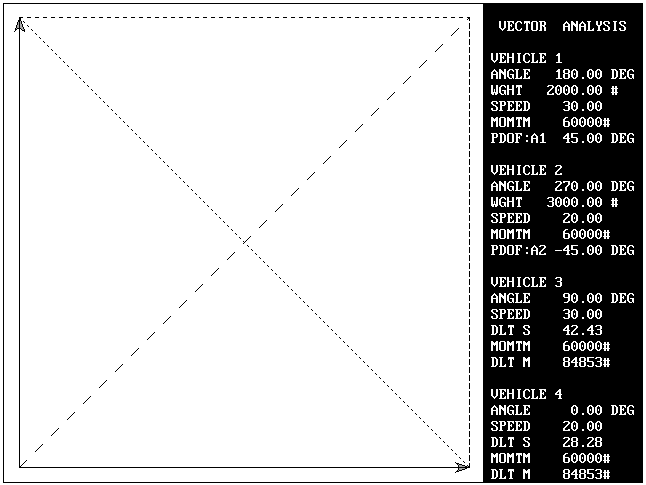
Problem 1B: This is basically the same problem with a few minor differences. Impact velocities and angles are given as well as the fact that the two vehicles remain together from impact until final rest.
If the vehicles remain together from impact until final rest, the departure angles for vehicle #1 (A3) and vehicle #2 (A4) are identical as are the post impact velocities.
Total momentum (Mr) at impact = SQR(Mx^2 + My^2)
Mr = SQR((2000*30)^2 + (3000*20)^2 = 84,852.81
The conservation of linear momentum states that the total momentum after collision must equal the total momentum before collision.
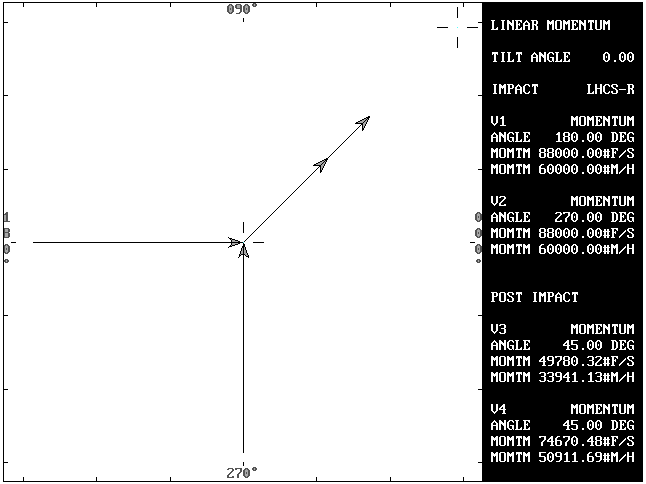
Total momentum after collision (Mr) = 84,852.81
The resultant vector has a direction. The orientation angle of the vector is the arctangent of the Y component divided X component.
arctangent(60,000/60,000) = atn(1) = 45 degrees
The departure angle for both vehicles is 45 degrees.
Since the vehicles remained together, the velocity is the resultant momentum (Mr) divided by the weight of both vehicles.
Velocity = Mr/(W1+W2) = 84852.81/(2000+3000)
V3 and V4 = 16.9705
The resultant momentum vectors must be equal in both magnitude and direction for both impact and post impact. This is true even when the exit vehicles do not have identical angles and/or velocities.
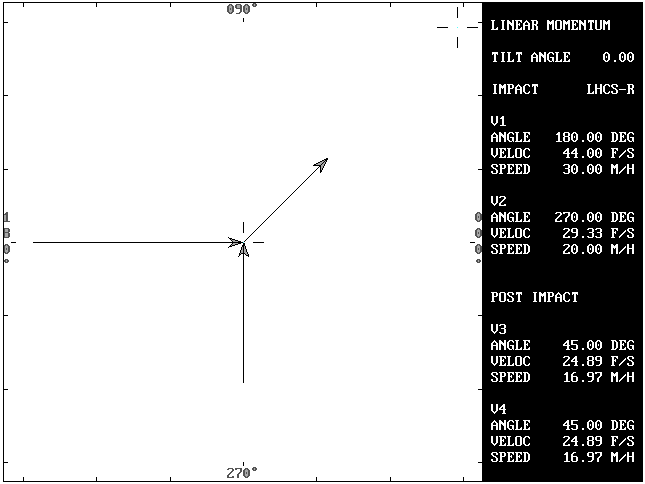
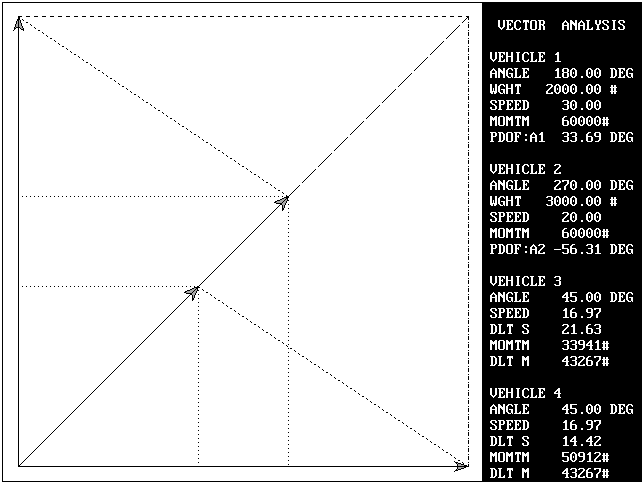
Problem 1C: This problem will be basically the same as Problem 1B, except that the departure angles and velocities are (for the moment) unknown.
Based on the formulae in problem 1B , the resultant momentum vector has an orientation angle of 45 degrees and a magnitude of 84,852.81.
Angle A3 (60 degrees) and angle A4 (30 degrees) will be treated as given. This information will be used to solve for M3 and M4 using the Law of Sines. The velocities (V3 and V4) can be obtained by dividing by the respective weights.
Law of Sines: sin(angle a)/A = sin(angle b)/B = sin(angle c)/C
The following is known:
side A = M3
side B = M4
side C = Mr = 84,852.81
angle a = (60 - 45) = 15 degrees
angle b = (45 - 30) = 15 degrees
angle c = 180 - angle a - angle b = 150 degrees
Solving for M3 and M4:
M4 = Mr * sin(a) / sin(c) = 43,923.05
M3 = M4 * sin(b) / sin(a) = 43,923.05
V3 = M3 / W1 = 21.9615
V4 = M4 / W2 = 14.6410
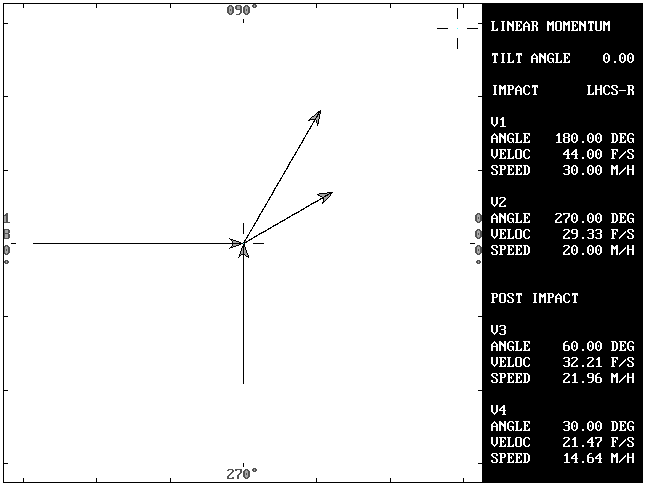
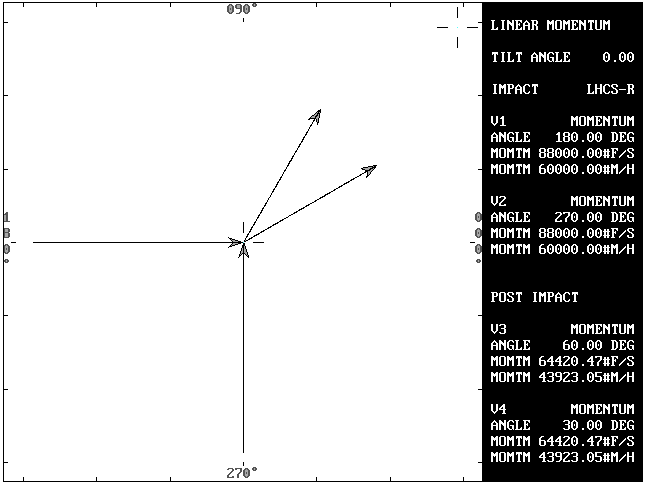
Problem 2: Post impact velocities of both vehicles are given. Post impact angles will be determined using the Law of Cosines.
Law of Cosines:
A^2 = B^2 + C^2 - 2 * B * C * cos(angle a)
B^2 = A^2 + C^2 - 2 * A * C * cos(angle b)
C^2 = A^2 + B^2 - 2 * A * B * cos(angle c)
Using the formulae in problem 1B, the length of the resultant vector can be determined.
The length of all three (3) sides of the triangle are known.
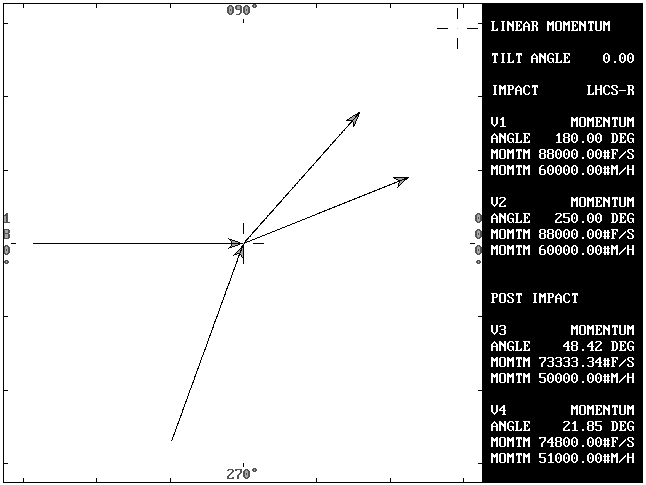
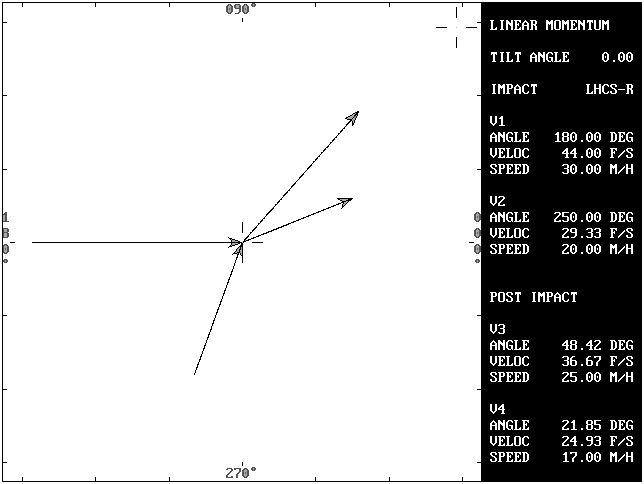
Solving for the angles (A3 and A4):
My = sin(250)*60,000 = -56,381.56
Mx = cos(180)*(2000*30) + cos(250)*(3000*20) = -80,521.21
Mr = SQR(Mx^2 + My^2) = 98,298.25
M3 = V3 * W1 = 25*2000 = 50,000
M4 = V4 * W2 = 17*3000 = 51,000
Orientation angle = angle c = atn(My/Mx) = 35
ANGLE a = inverse cos((M3^2 + Mr^2 - M4^2) / (2*M3*Mr)) = 13.42
ANGLE b = inverse cos((M4^2 + Mr^2 - M3^2) / (2*M4*Mr)) = 13.15
A3 = angle a + angle c = 48.42 degrees
A4 = angle c - angle b = 21.85 degrees
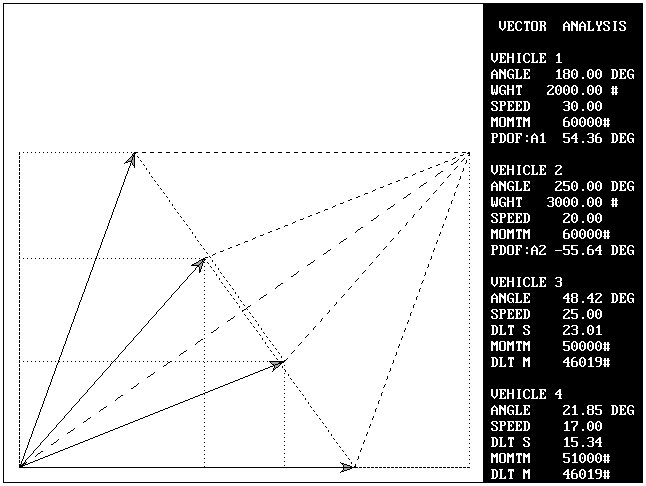
Problem 3A: The post impact velocity (V3) and departure angle (A3) of vehicle #1 are given. The post impact velocity (V4) and departure angle (A4) of vehicle #2 will be determined using the Law of Cosines.
Using the formulae in problem 1B, the length of the resultant vector can be determined.
The length of two (2) sides and one (1) angle of the triangle are known.
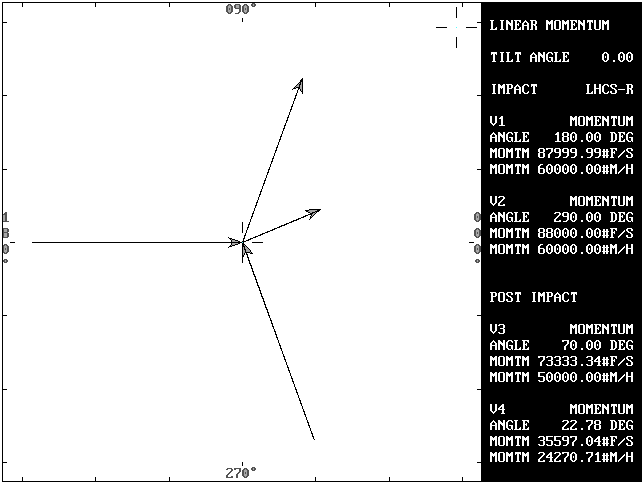
Solving for the side M4:
My = sin(290)*60,000 = -56,381.56
Mx = cos(180)*(2000*30) + cos(290)*(3000*20) = -39,478.79
Mr = SQR(Mx^2 + My^2) = 68,829.17
M3 = V3 * W1 = 25*2000 = 50,000
Orientation angle = angle c = atn(My/Mx) = 55
ANGLE a = angle A3 - angle c = 15 degrees
M4 = SQR(M3^2 + Mr^2 - (2 * M3 * Mr * cos (a))) = 24,270.71
V4 = M4/W2 = 24,270.71/3000 = 8.09
Knowing both M3 and M4 the solution for angle b is solved as it was in Problem 2 above using the Law of Cosines.
ANGLE b = inverse cos((M4^2 + Mr^2 - M3^2) / (2*M4*Mr)) = 32.22
A4 = angle c - angle b = 22.78 degrees
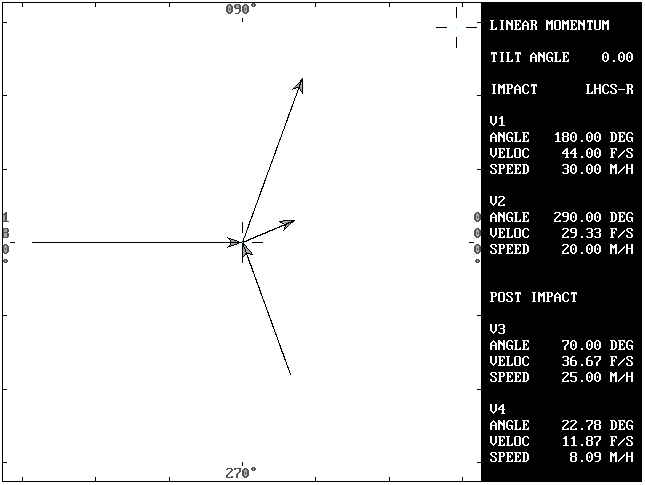
Problem 3A - Alternative solution: Vector component addition can also be used to solve problem 3A.
The total vertical momentum at impact must equal the total vertical momentum after impact.
Solving for the total vertical component of momentum after impact (Py):
Py = M1y + M2y = M3y + M4y
The vertical component of momentum for vehicle #1 at impact is zero (0).
Py = V2 * W2 * cos(A2) = -60,000 * sin(290) = 56,318.56
V1 * W1 * sin(A1) + V2 * W2 * sin(A2) = M3y + M4y
0 + (-30) * 2000 * sin(A2) = V3 * W1 * sin(A3) + M4y
-60000 * sin(290) = 25 * 2000 * sin(70) + M4y
M4y = 56,381.56 - 46,984.63
M4y = 9396.95
Solving for the total horizontal component of momentum after impact (Px):
Px = M3x + M4x = M1x + M3x
Px = V1 * W1 * cos(A1) + V2 * W2 * cos(A2)
Px = -30 * 2000 * cos(180) + (-20) * 3000 * cos(290)
Px = 60,000 - 20,521.21 = 39,478.79
M3x = M3 * cos(A3) = V3 * W1 * cos(A3)
M3x = 25 * 3000 * cos(70) = 17,101.07
M4x = P4x - M3x = 39,478.79 - 20,521.21 = 22,377.78
M4 = SQR(M4x^2 + M4y^2) = 24,270.72
V4 = M4 / W2 = 24,270.72 / 3000
V4 = 8.09
A4 = atn(M4y/M4x) = atn(9396.95 / 22,377.78)
A4 = 22.78 degrees

Problem 3B: The post impact velocity of vehicle #1 (V3) and departure angle of vehicle #2 (A4) are given. The post impact velocity of vehicle #2 (V4) and the departure angle of vehicle #1 (A) will be determined using the Law of Cosines.
Using the formulae in problem 1B, the length of the resultant vector can be determined.
Two (2) sides and one (1) angle of the triangle are known.
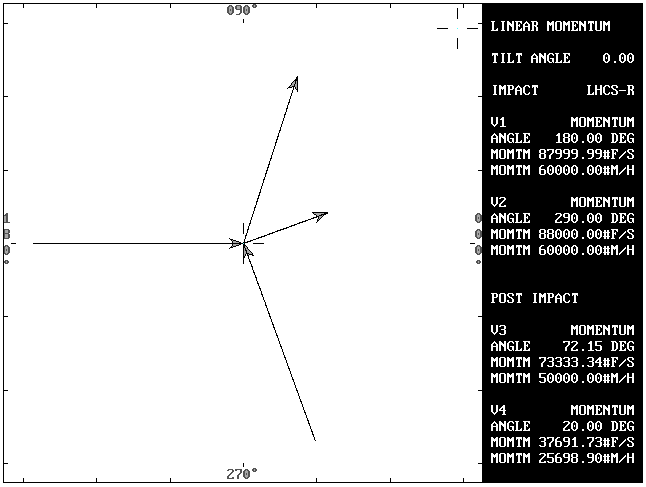
Solving for the third side (M4):
My = sin(290)*60,000 = -56,381.56
Mx = cos(180)*(2000*30) + cos(290)*(3000*20) = -39,478.79
Mr = SQR(Mx^2 + My^2) = 68,829.17
M3 = V3 * W1 = 25*2000 = 50,000
Orientation angle = angle c = atn(My/Mx) = 55
ANGLE b = angle c - angle A4 = 35 degrees
BB = 2 * Mr * cos (b) = 112,763.11
CC = Mr^2 - M3^2 = 2,237,454,968
Q1 = (BB - SQR(BB^2 - 4 * CC)) / 2 = 25,698.91
Q2 = (BB + SQR(BB^2 - 4 * CC)) / 2 = 87,064.21
Two (2) possible solutions, or roots, result from the quadratic formula. Both roots must be checked in order to determine which is the correct solution to the problem.
DETERMINATION OF THE CORRECT ROOT OF THE QUADRATIC:
If M4 = Q2 = 87.064.21 then:
V4 = M4/W2 = 87.064.21/3000 = 29.02
ANGLE a = inverse cos((M3^2 + Mr^2 - M4^2) / (2*M3*Mr)) = 92.15
A3 = angle c + angle a = 147.85 degrees
This angle is outside of the cone of departure (0 to 110 degrees) that is dictated by the approach angles(A1 = 180 and A2 = 290), therefore:
The correct root of the quadratic is:
M4 = Q1 = 25,698.91
V4 = M4/W2 = 25,698.9/3000 = 8.57
Knowing both M3 and M4 the solution for angle b is solved as it was in Problem 2 above.
ANGLE a = inverse cos((M3^2 + Mr^2 - M4^2) / (2*M3*Mr)) = 17.15
A3 = angle c + angle a = 72.15 degrees

Having completed vector momentum analysis, the reconstructionist should have a better understanding of linear momentum and vector sum analysis as well as a greater appreciation of the forces involved in the collision.
The graphics and mathematical computations used throughout this article were generated using REC-TEC Professional - Version V accident reconstruction software from REC-TEC LLC.
Copyright (C) 1993 George M. Bonnett, J.D. All Rights Reserved
206-375-0699 or 321-271-6459
REC-TEC LLC P.O. BOX 561031 ROCKLEDGE, FL 32956 USA
Copyright © George M. Bonnett, JD
Last edited on Monday, 17 January 2022 03:33:55 PM -0500